Coordinate Systems and Components of a Vector
2.2 Coordinate Systems and Components of a Vector
Learning Objectives
By the end of this section, you will be able to:
- Describe vectors in two and three dimensions in terms of their components, using unit vectors along the axes.
- Distinguish between the vector components of a vector and the scalar components of a vector.
- Explain how the magnitude of a vector is defined in terms of the components of a vector.
- Identify the direction angle of a vector in a plane.
- Explain the connection between polar coordinates and Cartesian coordinates in a plane.
Trig Review
Before we get into the discussion about vector components, let’s first do a quick review of trigonometry. Test yourself with the following practice problems.
Practice!
| Practice 2.2.1 |
|---|
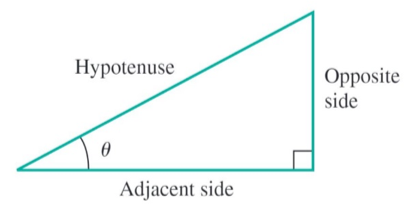 From the figure, how do you define the  ? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.2 |
|---|
From the figure, how do you define the  ? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.3 |
|---|
From the figure, how do you define the  ? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.4 |
|---|
 What is the length of the side of the triangle adjacent to θ if θ = 30° and the hypotenuse is 2 units? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.5 |
|---|
What is the length of the side of the triangle opposite to θ if θ = 30° and the hypotenuse is 2 units? |
| (a) |
| (b) |
| (c) |
| (d) |
| (e) |
| Practice 2.2.6 |
|---|
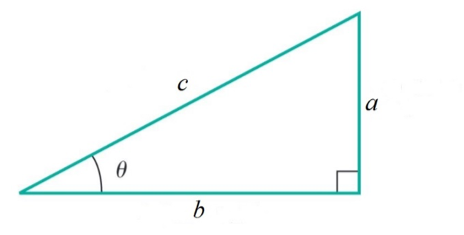 From the triangle in the figure, what is another way to express c? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
Vector Components
Practice!
| Practice 2.2.7 |
|---|
 What is the magnitude of the x-component of vector  ? |
| (a) 14.4 m |
| (b) 10.8 m |
| (c) 13.6 m |
| (d) 18.0 m |
| (e) 12.0 m |
| Practice 2.2.8 |
|---|
What is the magnitude of the y-component of vector ? |
| (a) 14.4 m |
| (b) 10.8 m |
| (c) 13.6 m |
| (d) 18.0 m |
| (e) 12.0 m |
Adding Vectors using Vector Components
Practice!
| Practice 2.2.9 |
|---|
When vector  is added to vector , the resultant is vector  such that . = + . What is the magnitude of the x-component of the resultant vector ? |
| (a) 26.4 m |
| (b) 10.8 m |
| (c) 22.8 m |
| (d) 6.00 m |
| (e) 2.40 m |
| Practice 2.2.10 |
|---|
When vector is added to vector , the resultant is vector such that . = + . What is the magnitude of the y-component of the resultant vector ? |
| (a) 26.4 m |
| (b) 10.8 m |
| (c) 22.8 m |
| (d) 6.00 m |
| (e) 2.40 m |
| Practice 2.2.11 |
|---|
When vector is added to vector , the resultant is vector such that . = + . This resultant vector has components  and  . How do you determine the magnitude of ? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.12 |
|---|
When vector is added to vector , the resultant is vector such that . = + . This resultant vector has components and . How do you determine the direction of , the angle the vector makes with the positive x-axis? |
(a)  |
(b)  |
(c)  |
(d)  |
(e)  |
| Practice 2.2.13 |
|---|
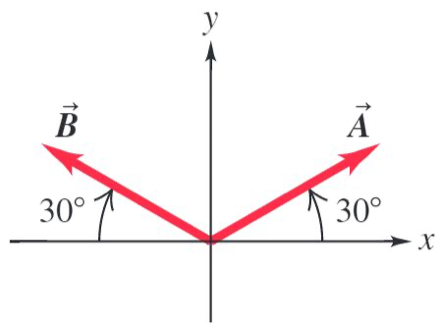 Vectors and have equal magnitudes but point in different directions, as shown in the figure. What is true about the x-component of vector compared to the x-component of vector ? |
(a)  is equal in magnitude and points in the same direction to  . |
| (b) is greater in magnitude and points in the opposite direction to . |
| (c) is greater in magnitude and points in the same direction to . |
| (d) is equal in magnitude and points in the opposite direction to . |
| Practice 2.2.14 |
|---|
Vectors and have equal magnitudes but point in different directions, as shown in the figure. What is true about the y-component of vector compared to the y-component of vector ? |
(a)  is equal in magnitude and points in the same direction to  . |
| (b) is greater in magnitude and points in the opposite direction to . |
| (c) is greater in magnitude and points in the same direction to . |
| (d) is equal in magnitude and points in the opposite direction to . |
| Practice 2.2.15 |
|---|
Vectors and have equal magnitudes but point in different directions, as shown in the figure. If you add + , what is true about the resultant vector = + ? |
(a) The resultant  points in the positive y-direction and has a magnitude equal to A + B. |
| (b) The resultant points in the positive x-direction and has a magnitude less than A + B. |
| (c) The resultant points in the positive x-direction and has a magnitude equal to A + B. |
| (d) The resultant points in the positive y-direction and has a magnitude less than A + B. |
| (e) The resultant points in the negative x-direction and has a magnitude less than A + B. |
Discuss!
Consider how you would answer this question. Then bring this to class for a group discussion.
An ant crawling on a table undergoes three consecutive displacements:
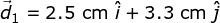
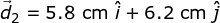
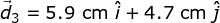
Find the magnitude and direction of the resultant displacement.
Physics Education Research at UNG 