Interference in Thin Films

15.4 Interference in Thin Films
Learning Objectives
By the end of this section, you will be able to:
- Describe the phase changes that occur upon reflection
- Describe fringes established by reflected rays of a common source
- Explain the appearance of colors in thin films
Thin Film Interference
To explain why soap bubbles are swirly and iridescent, and why the Blue Morpho butterfly’s wings are blue, we will use thin film interference. Another way to describe this is interference by reflection. So let’s begin by talking about what happens to a wave when it reflects from a boundary between different mediums.
Reflection of Waves
We’re going to use a wave pulse traveling on a string as an analogy for a light wave traveling in a material. When the wave travels in a thin string, it’s like a light wave traveling in a medium with a small index of refraction. And when the wave travels in a thick string, it’s like a light wave traveling in a medium with a large index of refraction.
Let’s take a thin string and attach it to a thick string, and send a wave pulse from left to right like this:

Imagine this is like light traveling in air and then reaching a boundary between the air and a denser material, let’s say glass. When the light wave gets to the boundary, some of it will transmit into the glass and some will reflect. Watch what happens to the wave when it reflects from the denser medium:
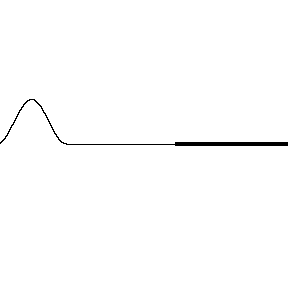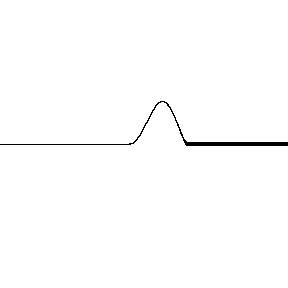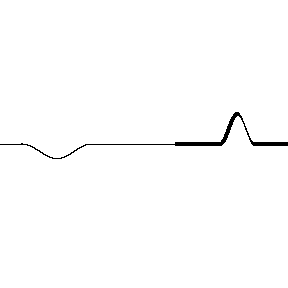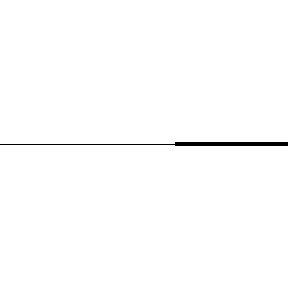
The wave pulse flips upside down. What this means is the reflected wave is shifted out of phase with the incident wave, shifted by 180° or half a wavelength.
Rule 1: When a light wave travels in a medium with a small index of refraction and reflects from a medium with a larger index of refraction, the reflected wave will be out of phase with the incident wave.
Watch what happens to the wave when it starts by traveling in the denser medium and reflects from the less dense medium:

The reflected wave doesn’t flip upside down this time. So the reflected wave is is phase with the incident wave, there is no phase shift upon reflection.
Rule 2: When a light wave travels in a medium with a large index of refraction and reflects from a medium with a smaller index of refraction, the reflected wave will be in phase with the incident wave.
Thin Film Interference: Soap Bubble
So let’s use these rules for the reflection of light to explain why a soap bubble looks like this:

Here is a really cool video that shows how the thickness of a thin soap film affects the wavelengths you can see:
By holding the soap film vertically, gravity pulls downward on the film, making the film get gradually thicker on the bottom and thinner on the top. The thickness of the film determines the wavelength of light that you can see. Eventually, the film gets so thin that you can’t see visible wavelengths anymore and the film appears completely transparent.
Imagine that you could slice this soap film and look at a cross section of the film. Here is my depiction of that cross section of the film:

The blue part is the soap film, with thickness equal to t. Soap is mostly water so its index of refraction is 1.33. On either side of the film (above and below) is air, so the index of refraction of the medium above and below the soap film is n = 1 (air). Light is going to travel in the air and then be incident on the film. Some of that incident light will reflect from the surface of the soap film and some will transmit into the soap film. We will look at what happens to those light rays.

To determine if we see a bright fringe reflecting from the soap film, we need to determine if ray (1) and ray (2) are in phase or out of phase when they reach our eyes. Ray (2) travels a longer distance than ray (1) does — it travels into the film and out again, which ray (1) does not do. So the path difference between rays (1) and (2) is the thickness of the film + the thickness of the film, or t + t = 2t. Now we need to determine if ray (2) is in phase with ray (1) after traveling this longer distance.
When ray (2) travels in the soap film, it’s wavelength changes because the light slows down. The wavelength of ray (2) is
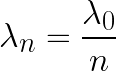
when it is in the soap film, where λ0 is the wavelength when in the air and n is the index of refraction of the soap film.
When ray (2) reflects at point B, it doesn’t experience a phase shift because it is reflecting from air, which has a lower index of refraction than the soap film. But when ray (1) reflects at point A, it DOES experience a phase shift because it reflects from a medium with a higher index of refraction. (The reflection at A is like the wave pulse traveling in the thin string and reflecting from the thick string, while the reflection at B is like the pulse traveling in the thick string and reflecting from the thin string.)
For ray (1) and ray (2) to be in phase and constructively interfere when they reach our eyes, we need the path difference (2t) to be equal to at least half a wavelength of ray (2) while it’s in the soap film. This is because of that phase shift at A. If the path difference was equal to a whole wavelength, then (1) and (2) would be out of phase when they reach our eyes because of that phase shift at A.
So the condition for constructive interference is:

where 2t is the path difference between (1) and (2), λn is the wavelength of (2) while it travels in the soap film, and m is an integer (m = 0, 1, 2, …). We can sub in the equation for λn to get:

where n is the index of refraction of the soap film.
What this equation tells us is the thicknesses of the film that correspond to the wavelengths you will see reflected from the film.

Practice!
| Practice 15.4.1 |
|---|
| Light of frequency 6.00 × 1014 Hz illuminates a soap film (n = 1.33) having air on both sides of it. When viewing the film by reflected light, what is the minimum thickness of the film that will give an interference maximum when the light is incident normally on it? |

Discuss!
Calculate the minimum thickness of a soap-bubble film (n = 1.33) that results in constructive interference in the reflected light if the film is illuminated with light whose wavelength in air is λ = 460 nm. What are the next two thinnest film thicknesses that will produce constructive interference?
Antireflective Coating

Practice!
| Practice 15.4.2 |
|---|
The antireflective glass shown is covered with a thin layer of magnesium fluoride (n = 1.38). The index of refraction of the glass is 1.52. What minimum thickness of magnesium fluoride is needed to cause destructive interference of light whose wavelength is in the middle of the visible range at 555 nm? |
| Practice 15.4.3 |
|---|
| A thin layer of oil (n = 1.25) is floating on water (n = 1.33). What is the minimum nonzero thickness of the oil in the region that strongly reflects green light (λ = 530 nm)? |
Structural Color

OK, finally we get to learn about what makes the Blue Morpho butterfly blue. I’ve found a few videos that describe it well and I hope you enjoy them as much as I do. Structural color in nature is one of the most fascinating things about evolution, in my opinion.