PHYS 2212 Module 5.2

Model of Conduction in Metals

Recommended Reading

5.2 Model of Conduction in Metals

Learning Objectives

By the end of this section, you will be able to:

  • Define the drift velocity of charges moving through a metal
  • Define the vector current density
  • Describe the operation of an incandescent lamp

Current Density

Practice!

Practice 5.2.1
A copper cylinder is machined to have the following shape.  The ends are connected to a battery so that a current flows through the copper.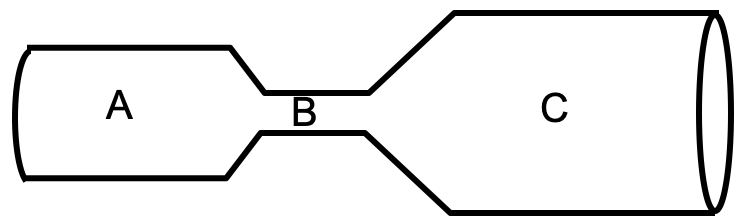

Which region has the greatest current density ?
Check your answer: B. region B
Practice 5.2.2
A copper cylinder is machined to have the following shape.  The ends are connected to a battery so that a current flows through the copper.

Which region has the greatest magnitude of current, I?
Check your answer: D. All three are the same
Practice 5.2.3
A copper cylinder is machined to have the following shape.  The ends are connected to a battery so that a current flows through the copper.

Which region has the greatest conductivity ?
Check your answer: D. All three are the same
Practice 5.2.4
A copper cylinder is machined to have the following shape.  The ends are connected to a battery so that a current flows through the copper.

Which region has the greatest magnitude electric field ?
Check your answer: B. region B
Practice 5.2.5
So far, we have concluded J is greatest in region B. (Using , and )
The ratio of diameters is A:B:C = 3:1:5.

How much larger magnitude is the drift velocity vd in region B compared to C?
Check your answer: B. 25x greater

Discuss!

An 18-gauge copper wire (the size usually used for lamp cords), with a diameter of 1.02 mm, carries a constant current of 1.67 A to a 200-W lamp. The free-electron density in the wire is 8.5 x 1028 electrons per cubic meter. Suppose we replaced the wire with 12-gauge copper wire, which has twice the diameter of 18-gauge wire. If the current remains the same, what effect would this have on the magnitude of the drift velocity vd?