Motion of a Charged Particle in a Magnetic Field

7.3 Motion of a Charged Particle in a Magnetic Field
Learning Objectives
By the end of this section, you will be able to:
- Explain how a charged particle in an external magnetic field undergoes circular motion
- Describe how to determine the radius of the circular motion of a charged particle in a magnetic field
Think about what might happen if a charged particle moves at a constant speed (v) into a uniform magnetic field (B). It will experience a magnetic force:
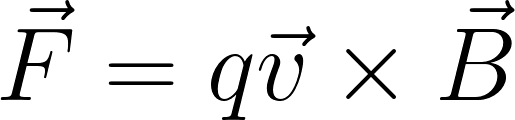

and the direction of this force is determined using the right hand rule.
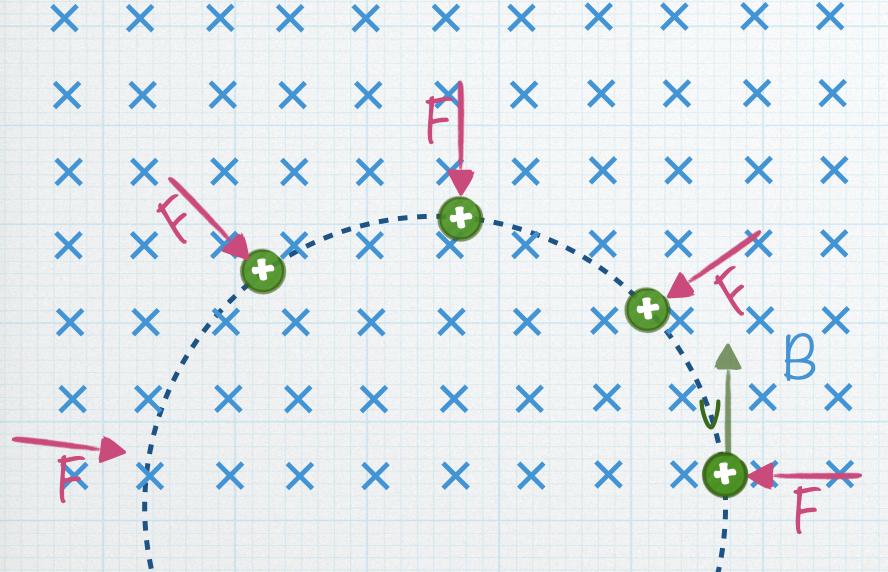
The force, by definition, is always perpendicular to the velocity and, as a result, the particle moves in a circular path. Notice how the force always points toward the center of the circular path. This type of force – pointing toward the center of a circular path – is called a centripetal force, and you talked about this in PHYS 2211. It’s a force that changes the direction of the velocity but doesn’t change the speed (because it’s always perpendicular to the velocity).
You’ll need to recall from PHYS 2211 that the centripetal acceleration (which comes from a centripetal force) is

where v is the speed of the object and r is the radius of the circular path. We can use Newton’s 2nd law:

and substitute the magnetic force in for the net force (since it is the only force acting on the particle) and substitute the centripetal acceleration for a:
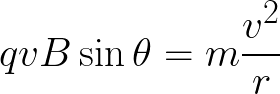
But the angle between v and B is always 90°, because the B-field is into the page and the velocity is parallel to the page. So sin 90° = 1 and we get:

We can then rearrange this to solve for any variable in the equation, but usually what we find is the radius of the circular path:


Practice!
The drawing shows the top view of two interconnected chambers. Each chamber has a unique magnetic field. A positively charged particle is fired into chamber 1, and observed to follow the dashed path shown in the figure.

| Practice 7.3.1 |
|---|
| What is the direction of the magnetic field in chamber 1? |
| Practice 7.3.2 |
|---|
| What is the direction of the magnetic field in chamber 2? |
| Practice 7.3.3 |
|---|
| Compare the magnitude of the magnetic field in chamber 1 to the magnitude of the magnetic field in chamber 2. |

Discuss!

A dust particle has a mass of 5.70×10−20 kg and a net charge of +4.80×10−19 C. It is observed to travel in a circular path of radius 1.45 cm in the magnetic field shown. What is the particle’s speed?
Mass Spectrometry
One application of this concept is in mass spectrometry. Many of you will use a mass spectrometer at some point so we will look at an example here to give you a better idea of the physics behind how it works. If you want to read more about mass spectrometry, you can do so here.
A mass spectrometer separates molecules based on something called the charge-to-mass ratio, which is literally the molecule’s charge divided by its mass: q/m. If you look at the equation we derived above, there is a charge-to-mass ratio in it:

So if we send charged molecules into a uniform magnetic field, we can solve for the charge-to-mass ratio:
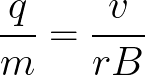
We will need to measure the radius of the circular path, the speed of the molecules, and the strength of the magnetic field, and then we can get q/m. What’s neat about this is the charge-to-mass ratio is unique for every molecule so we can identify unknown molecules with it. Basically, you send a bunch of different molecules into the magnetic field and they travel along different circular paths because they have different q/m values. We measure the radius of the path and identify the molecule.

In this next example, we will find the mass of a hydrogen ion using a mass spectrometer. This mass spectrometer is testing a hydrogen molecule (H2+) having charge +e. What is its mass?

We are given the radius, the strength of the magnetic field, and the amount of charge, so we know r, B, and q. But we don’t know how fast it’s moving, we don’t know v. We will need this to find m.
The ion is accelerated through a potential difference of 2400 V before it enters the magnetic field. Assuming the ion starts from rest as it enters this potential difference, we can solve for its speed after it moves through this ΔV.
Try working through this problem on your own, then you can watch my video solution to check your work.
Velocity Selector
To regulate the speed of the charges that move into a magnetic field in a mass spectrometer, sometimes a velocity selector is used. A velocity selector utilizes crossed electric and magnetic fields to allow charges with only one particular speed to pass through. Watch this video to see how this works: