Ampère’s Law
8.5 Ampère’s Law
Learning Objectives
By the end of this section, you will be able to:
- Explain how Ampère’s law relates the magnetic field produced by a current to the value of the current
- Calculate the magnetic field from a long straight wire, either thin or thick, by Ampère’s law
Ampère’s law
A fundamental property of a static magnetic field is that, unlike an electrostatic field, it is not conservative. A conservative vector field is one whose line integral between two end points is the same regardless of the path chosen. Magnetic fields do not have such a property. Instead, there is a relationship between the magnetic field and its source, electric current. It is expressed in terms of the line integral of 
and is known as Ampère’s law.
Practice!
| Practice 8.5.1 |
|---|
Evaluate the integral 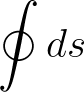 around a circular loop. |
| A. 0 |
| B. 2πR |
| C. πR2 |
| D. not enough information |
| Practice 8.5.2 |
|---|
Evaluate the integral 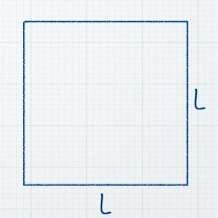 around a square loop. |
| A. 0 |
| B. L2 |
| C. 4L |
| D. not enough information |
| Practice 8.5.3 |
|---|
Two identical Amperian loops are drawn in proximity to two identical current carrying wires. For which loop is 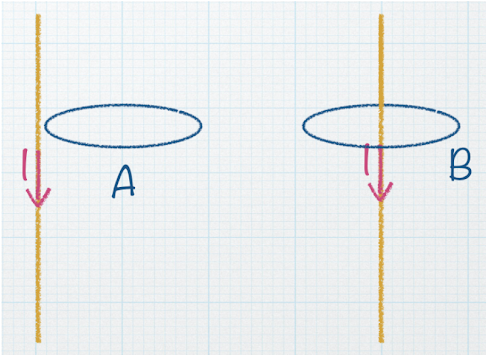 the greatest? |
| Practice 8.5.4 |
|---|
Now compare loops B and C. For which loop is 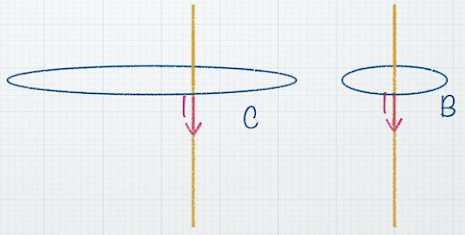the greatest? |
| Practice 8.5.5 |
|---|
An Amperian loop is drawn around two current carrying wires. What is the value of , moving counterclockwise around the loop when viewed from above? |
| A. µ0I1 |
| B. µ0I2 |
| C. µ0(I1 + I2) |
| D. µ0(I1 – I2) |
| E. 0 |
| Practice 8.5.6 |
|---|
An irregularly shaped Amperian loop is drawn around a wire carrying a current I. What is the value of 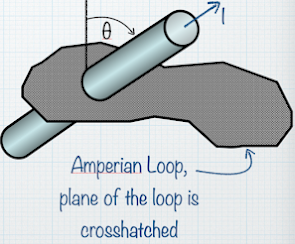, moving counterclockwise around the loop when viewed from above? |
| A. µ0I |
| B. -µ0I |
C. µ0I sin |
| D. µ0I cos |
| E. µ0I tan |
| F. 0 |
Physics Education Research at UNG 