Invariance of Physical Laws

1.1 Invariance of Physical Laws
Learning Objectives
- Describe the theoretical and experimental issues that Einstein’s theory of special relativity addressed.
- State the two postulates of the special theory of relativity.
Physics and Einstein circa 1900:
Selected Events and Trends of Significance in Physics, 1800-1900

Discuss!
Reflect on the given scenario and take notes on how you would approach this thought experiment. Then we will share these thoughts together in a class discussion.
Imagine: You wake up inside a room with no windows and one locked door (you checked). You cannot see outside. Looking around you see a table with a number of items on it: a desk lamp (plugged in and turned on), a tennis ball, a bunch of string, a pitcher of water and a cup, a candle, a box of matches, and a music player with headphones. A skateboard and a wooden stool are also in the room.
The music player has a sign on it saying “Turn on for instructions,” so you do. You are told that you are in a specially designed vibration-proof and noise-proof train car on a set of straight and level train tracks. Your task is to use one or more of the items in the room, perhaps in combination with each other, to determine whether the train car is stationary or is moving on the tracks. There is a thirty-minute time limit for your test (or tests), and destroying or modifying the walls, floor, or ceiling of the car is not permitted.
Can you think of some creative ways to use the items that might indicate whether you are moving? (Spoiler alert: The principle of relativity asserts that there is no way for you to tell whether the train car is moving. So once you think of some creative ways that might seem to be able to tell you whether you are moving, think about why they fail to do so. If you have a car, you might even try some experiments in it while it is stationary and while it is moving, with a friend driving, not yourself!)
Inertial Reference Frame
An inertial frame of reference is a reference frame in which a body at rest remains at rest and a body in motion moves at a constant speed in a straight line unless acted upon by an outside force.
Events, Clocks, and Observers
Consider an event that has occurred recently in your life (whether significant or mundane), or any event that occurs. What are the ways that we differentiate that event from some other event? What does it mean to say that someone “observed” or “recorded” an event? That is, what criteria must be satisfied by someone to be a good observer and/or recorder?
Before viewing the video on “Events, clocks, and observers,” consider the following thought experiment:
Consider two railway stations. One of them is exactly 25 kilometers to the east of the main railway station, and the other is exactly 25 kilometers to the west of the main station. (The tracks between them are straight and the ground is level, so the distances are straight-line distances.) Outline at least two methods by which you can make sure that the clocks at each outlying station are exactly synchronized with the clock at the main station.
Thought Experiment

Practice!
| Practice 1.1.1 |
|---|
| What is the simplest scientific meaning of the phrase “time is the fourth dimension”? |
| A. That an event that occurs in space and time can be described by three coordinates (x,y,z) representing the spatial location and a fourth coordinate representing the time the event occurs. |
| B. That an event that occurs can be specified using a lattice of four clocks. |
| C. That there are four dimensions of time, only one of which we experience. |
| D. That time travel is possible. |
| Practice 1.1.2 |
|---|
| What is the “photo clock principle”? |
| A. The idea that clocks cannot be synchronized without taking a photograph of them. |
| B. The idea that observing an event means to record its time and location using an (imaginary) clock at that location. |
| C. The idea that photographs cannot be trusted if they don’t have a timestamp on them. |
| D. The idea that an event only occurs if a photograph of it exists. |
| Practice 1.1.3 |
|---|
| One way to synchronize a system of identical (and well-running) clocks is to use one master clock to set the other clocks, and then move the clocks to their various locations. What is a potential problem with this approach that was mentioned in the video? |
| A. The act of moving the clocks will affect how they keep time compared to one another. |
| B. The master clock cannot be counted on to keep good time. |
| C. The other clocks cannot be counted on to keep in synchronization with each other after they are set. |
| D. None of the above. |
Frames of Reference and Spacetime Diagrams

Practice!
| Practice 1.1.4 |
|---|
| Which world line (in red) represents an object moving to the right at constant velocity along the x axis? |
A. 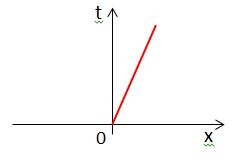 |
B. 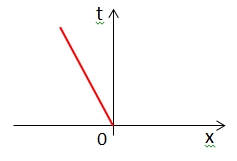 |
C. 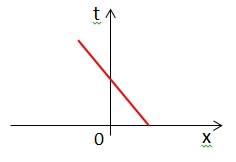 |
D. 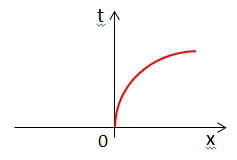 |
| Practice 1.1.5 |
|---|
| Which world line (in red) represents an object moving to the left at constant velocity along the x axis? |
A.  |
B.  |
C. 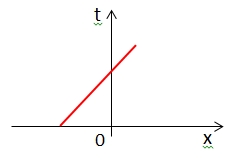 |
D.  |
| Practice 1.1.6 |
|---|
| Which world line (in red) represents an object that started at a nonzero location on the x axis and then moved to the right at constant velocity? |
A.  |
B.  |
C.  |
D.  |
| Practice 1.1.7 |
|---|
| Which world line (in red) represents an object that is moving with a varying velocity along the x axis? |
A.  |
B.  |
C.  |
D.  |
Two Postulates of Special Relativity
In 1905 (the “miracle year”), Einstein published four very important papers while he was working in a Swiss patent office. In one of those papers he describes the theory of special relativity. Here is a link to that paper (translated from German to English):
On the Electrodynamics of Moving Bodies
In the 2nd paragraph of this paper, Einstein presents two postulates of special relativity. In this course we will delve deeper into these postulates and learn about what they mean and how we apply them.
The laws of physics are the same in all inertial frames of reference.
First postulate of Special relativity
Light travels in a vacuum with the same speed c in any direction in all inertial frames.
Second postulate of special relativity