Time Dilation
| Practice 1.3.3 |
|---|
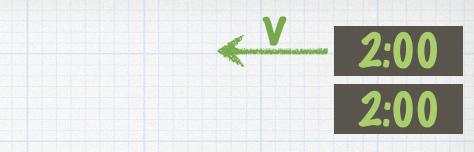 Two identical clocks are set to the same time as one passes the other at high velocity. Which of the figures represents a possible observation of the clocks at some later time in the frame of the fixed clock? |
 |
 |
 |
 |
 |
The Lorentz factor is given as:

where v is the relative speed between observers’ reference frames and c is the speed of light.
Calculate the Lorentz factor for different speeds, v. Start with a speed of about 1 km/s and increase from there. Create of plot of the Lorentz factor versus v. For what value of v will the Lorentz factor be significant? In other words, what speed v should be considered “relativistic”?
| Practice 1.3.5 |
|---|
| Given that muons travel at 0.998 times the speed of light when they are created in the upper atmosphere by cosmic rays, why is it surprising that they reach the surface of Earth? |
| A. Because they’re traveling so fast that they go right through the Earth |
| B. Because muons are repelled by Earth’s magnetic field |
| C. Because their mean lifetime would seem to be too short, i.e., even at that high speed, they would not make it to the surface of the Earth before decaying into other particles |
| Practice 1.3.6 |
|---|
| From the perspective of a person at the surface of Earth, how does the special theory of relativity explain how the muons make it down to the surface? |
| A. The person observes the muon’s velocity to speed up by the Lorentz factor, so that it gets down to the surface of the Earth more quickly than it otherwise would |
| B. The person observes the distance from the upper atmosphere to the surface of the Earth to be shortened, due to length contraction, so the muon doesn’t have to travel as far as it otherwise would |
| C. The person observes the muon’s internal “clock” running more slowly than when the muon is at rest, due to time dilation, so the moving muon stays intact longer than it otherwise would |
| Practice 1.3.7 |
|---|
| From the perspective of a muon, how does the special theory of relativity explain how it makes it down to the surface? |
| A. In the muon’s frame of reference, its internal “clock” runs more slowly than when the muon is at rest, due to time dilation, so the moving muon stays intact longer than it otherwise would |
| B. In the muon’s frame of reference, the distance from the upper atmosphere to the surface of the Earth is shortened, due to length contraction, so the muon doesn’t have to travel as far as it otherwise would |
| C. In the muon’s frame of reference, the muon’s velocity increases by the Lorentz factor, so that it gets down to the surface of the Earth more quickly than it otherwise would |
| Practice 1.3.8 |
|---|
| An unstable particle (i.e. a radioactive nucleus) has a half life of 10-8 s when it is at rest. If we produce a beam of these particles traveling at 4/5 times the speed of light, how far on average will the particles travel before decaying? |
| A. About 1.4 m |
| B. About 2.4 m |
| C. About 4 m |
| D. They won’t decay once they are moving |
It should be noted that the same equations apply to your everyday life. The reason that you don’t notice them is that objects in your everyday life move much slower than the speed of light. Now let’s look at the differences in measurements between two frames moving relative to one another at a speed of 30 m/s (about 67 mph). Your calculator may not be able to store enough digits to work these problems accurately, so you may need to use the approximations from the binomial expansion.
What would be the difference between the time t measured by an observer moving at 30 m/s and a proper time t0 for a proper time interval of 1 hour (3600 s)? The answer is small but non-zero. You will need to find an expression for the time difference using the approximation from the binomial expansion before you substitute in the numbers; otherwise your calculator will just give zero.
Check your answer: 1.8 x 10-11 s