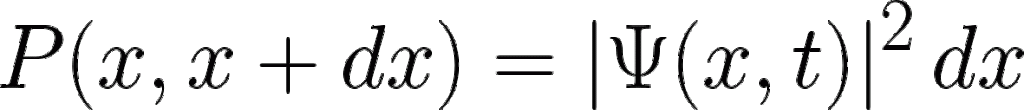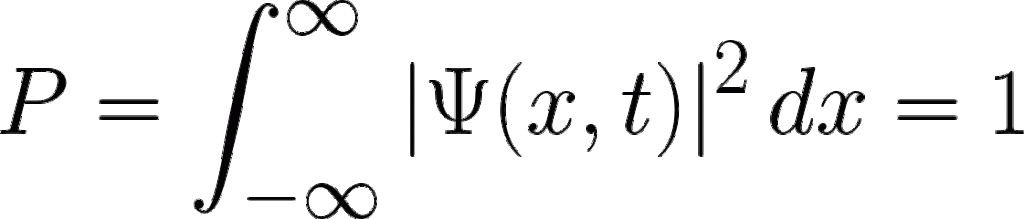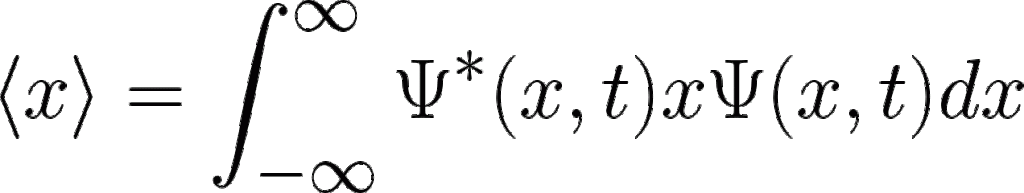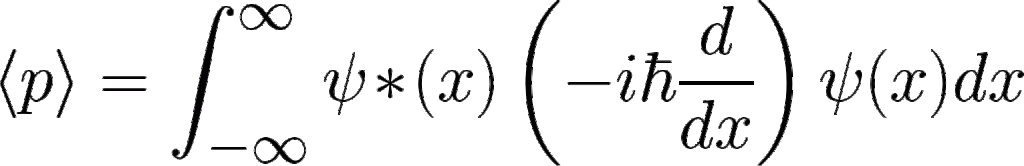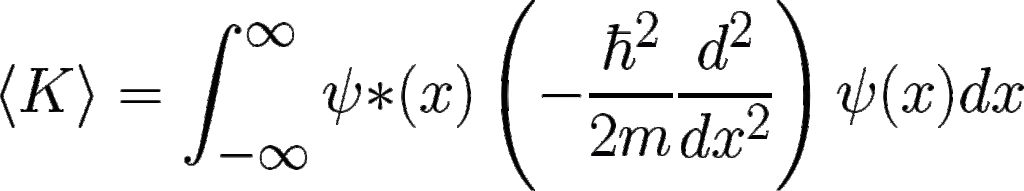PHYS 3310 Module 5.1

Wave Functions

Recommended Reading

5.1 Wave Functions

Learning Objectives

  • Describe the statistical interpretation of the wave function
  • Use the wave function to determine probabilities
  • Calculate expectation values of position, momentum, and kinetic energy

Probability Density

Probability to find a particle in a small interval (x, x + dx)

Practice!

Practice 5.1.1
Which of the following hypothetical wave functions for a particle in some realistic potential U(x) is acceptable?
A. (a)
B. (b)
C. (c)
D. more than one
E. none of them
Check your answer: B. (b)
Practice 5.1.2
Which of the following wavefunctions corresponds to a particle more likely to be found on the left side?
A. (a)
B. (b)
C. (c)
D. more than one
E. none of them
Check your answer: E. none of them

Normalizing the Wave Function

Normalization Condition

Discuss!

What is A when the wave function 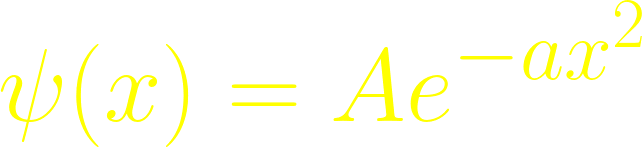is normalized?

Complex Conjugate

Discuss!

If 𝑎 = 3 + 4𝑖, what is the product 𝑎∗𝑎?

Suppose that a particle with energy E is moving along the x-axis and is confined in the region between 0 and L. One possible wave function is

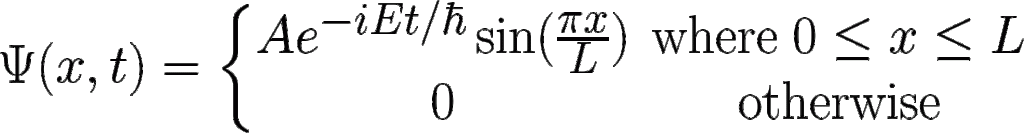
Determine the normalization constant.

Expectation Value

Expectation Value of Position

Expectation Value of Momentum

Expectation Value of Kinetic Energy