The Quantum Particle in a Box

6.1 The Quantum Particle in a Box
Learning Objectives
- Describe how to set up a boundary-value problem for the stationary Schrӧdinger equation
- Explain why the energy of a quantum particle in a box is quantized
- Describe the physical meaning of stationary solutions to Schrӧdinger’s equation and the connection of these solutions with time-dependent quantum states
- Explain the physical meaning of Bohr’s correspondence principle

Practice!
| Practice 6.1.1 |
|---|
| Consider an electron, a proton, and an alpha particle (a helium nucleus), each trapped separately in identical boxes. Which particle corresponds to the highest ground-state energy? |
| A. the electron |
| B. the proton |
| C. the alpha particle |
| D. The ground-state energy is the same in all three cases. |
| Practice 6.1.2 |
|---|
| Consider an electron, a proton, and an alpha particle (a helium nucleus), each trapped separately in identical boxes. Which particle has the longest wavelength when the system is in the ground state? |
| A. the electron |
| B. the proton |
| C. the alpha particle |
| D. All three particles have the same wavelength. |
| Practice 6.1.3 |
|---|
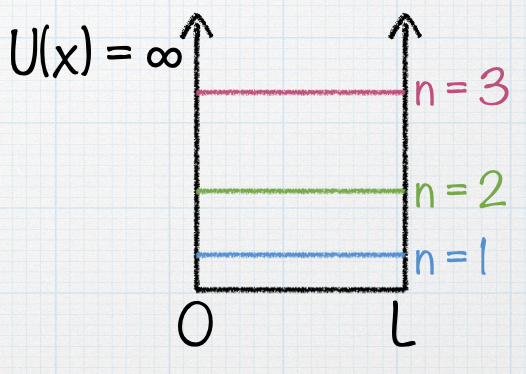 An electron is in a quantum “dot”. If we decrease the size of the dot, the ground state energy of the electron will |
| A. decrease |
| B. increase |
| C. remain the same |
| Practice 6.1.4 |
|---|
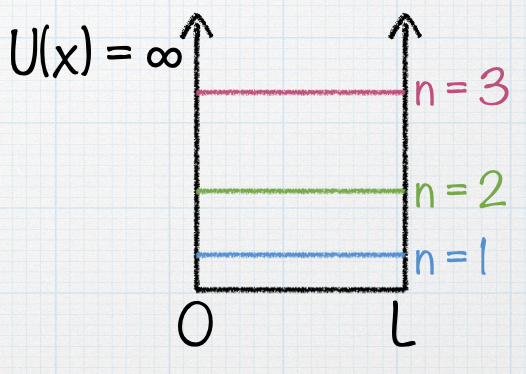 A particle is in a box of length L. Suddenly, the length of the box is increased to 2L. What happens to the energy levels shown in the figure? |
| A. Nothing; they are unaffected. |
| B. They move farther apart. |
| C. They move closer together. |

Discuss!
An electron is trapped in a “quantum wire” that is L = 4 nm long.
(a) Assuming that the potential seen by the electron is approximately that of an infinite square well, estimate the ground (lowest) state energy of the electron.
(b) What photon energy is required to excite the trapped electron to the next available energy level (i.e., n = 2)?
Properties of Bound States

Discuss!
The wavefunction below describes a quantum particle in a range Δx:
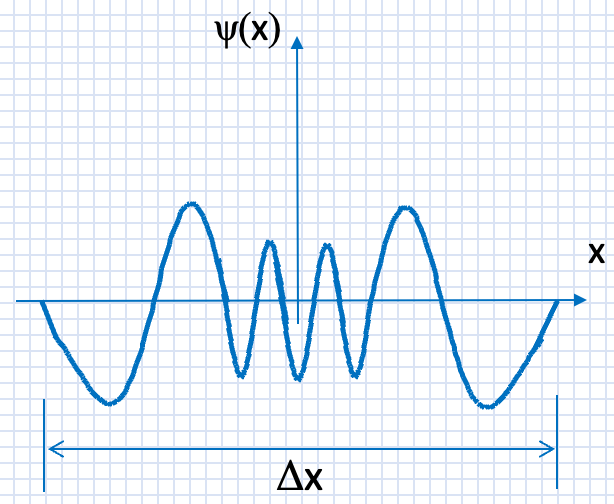
(a) In what energy level is the particle? n = ?
(b) What is the approximate shape of the potential U(x) in which this particle is confined?
