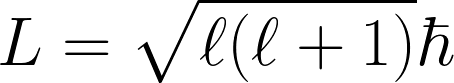PHYS 3310 Module 7.1

The Hydrogen Atom

Recommended Reading

7.1 The Hydrogen Atom

Learning Objectives

  • Describe the hydrogen atom in terms of wave function, probability density, total energy, and orbital angular momentum
  • Identify the physical significance of each of the quantum numbers (n, l, ml) of the hydrogen atom
  • Distinguish between the Bohr and Schrödinger models of the atom
  • Use quantum numbers to calculate important information about the hydrogen atom

Quantum Particles in 3-d Potentials

Practice!

Practice 7.1.1
Consider a particle in a two-dimensional (infinite) well, with Lx = Ly. Compare the energies of the (2,2), (1,3), and (3,1) states.
A. E(2,2) > E(1,3) = E(3,1)
B. E(2,2) = E(1,3) = E(3,1)
C. E(1,3) = E(3,1) > E(2,2)
Check your answer: C. E(1,3) = E(3,1) > E(2,2)
Practice 7.1.2
Consider a particle in a two-dimensional (infinite) well. If we squeeze the box in the x-direction (i.e., Lx < Ly) compare E(1,3) with E(3,1):
A. E(1,3) < E(3,1)
B. E(1,3) = E(3,1)
C. E(1,3) > E(3,1)
Check your answer: A. E(1,3) < E(3,1)

Energies for a particle in a 3-d box (equal sides of length a)

Discuss!

Draw an energy level diagram for a particle in a 3-d box with equal sides of length a.

(a) Show the energies and label (nx,ny,nz) for the first 11 states of the particle in the 3D box, and write the degeneracy D for each allowed energy. 

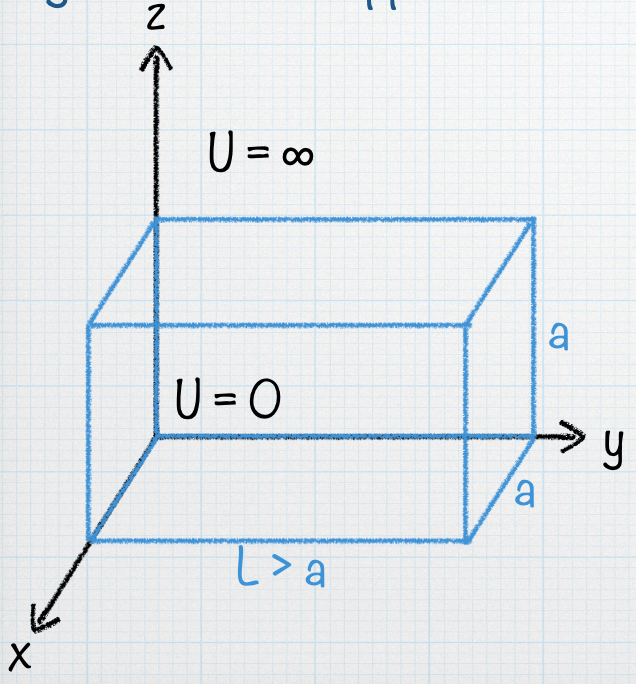
(b) Assume that the box is stretched only along the y-direction.  What do you think will happen to the cube’s energy levels?

The Hydrogen Atom

Quantized Energy

n = 1, 2, 3, …

Quantized Angular Momentum

ℓ = 0, 1, 2, …, n-1

Space Quantization of Angular Momentum

mℓ = -ℓ, …, -2, -1, 0, 1, 2, …, +ℓ

Quantum States of the Hydrogen Atom

Practice!

Practice 7.1.3
When the principal quantum number is n = 5, how many different values of ℓ are possible?
A. 0
B. 1
C. 2
D. 3
E. 5
F. 6
G. 9
Check your answer: E. 5
Practice 7.1.4
When the principal quantum number is n = 5. how many different values of mℓ are possible?
A. 0
B. 1
C. 2
D. 3
E. 5
F. 6
G. 9
Check your answer: G. 9
Practice 7.1.5
What angle does the orbital angular momentum make with the z axis of a hydrogen atom in the state n = 3, ℓ = 2, mℓ = –1?
A. -66°
B. 66°
C. 24°
D. 114°
E. 73°
Check your answer: D. 114°
Practice 7.1.6
A hydrogen atom in the 4f state has a total orbital angular momentum of
A. 2√3 ħ
B. 3 ħ
C. 6 ħ
D. √3 ħ
E. 12 ħ
Check your answer: A

Discuss!

For hydrogen in a 4f state:

(a) Find all the possible values of Lz

(b) Find all the possible values of θ

Hydrogenic Wave Functions