PHYS 3310 Module 8.1

Electron Spin

Recommended Reading

8.1 Electron Spin

Learning Objectives

  • Express the state of an electron in a hydrogen atom in terms of five quantum numbers
  • Use quantum numbers to calculate the magnitude and direction of the spin and magnetic moment of an electron
  • Explain the fine and hyperfine structure of the hydrogen spectrum in terms of magnetic interactions inside the hydrogen atom

Practice!

Practice 8.1.1

Consider a magnet in an inhomogeneous field, as shown.  Which way will the magnet feel a force?
A. up
B. down
C. left
D. right
E. no net force
Check your answer: A. up
Practice 8.1.2

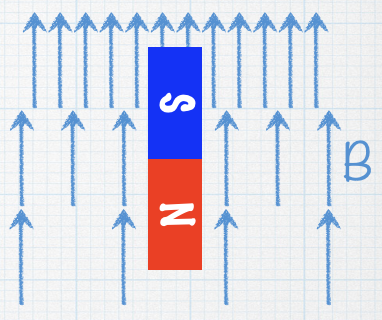Consider a magnet in an inhomogeneous field, as shown.  Which way will the magnet feel a force?
A. up
B. down
C. left
D. right
E. no net force
Check your answer: B. down
Practice 8.1.3

Consider a magnet in an inhomogeneous field, as shown.  Which way will the magnet feel a force?
A. up
B. down
C. left
D. right
E. no net force
Check your answer: E. no net force

Discuss!

If you send a beam of bar magnets through this inhomogeneous magnetic field and detect them on the other side, what will the distribution look like? 

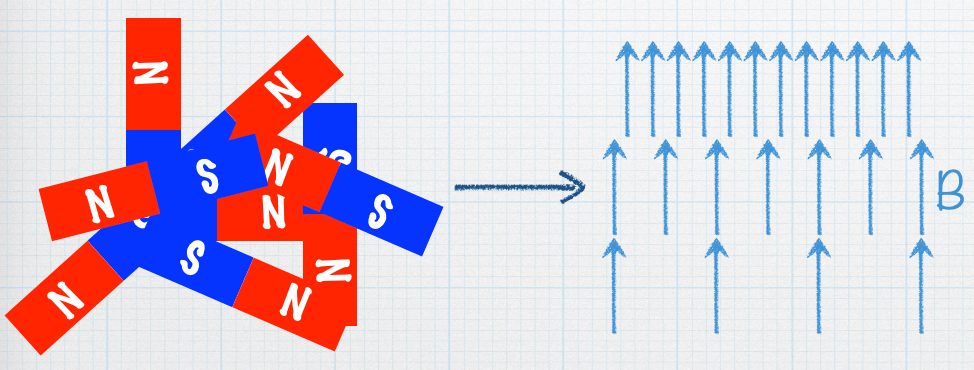
The Stern-Gerlach Experiment

Spin Angular Momentum

Practice!

Practice 8.1.3
In 1921, Stern and Gerlach performed an experiment that first demonstrated
A. orbital angular momentum quantization
B. energy quantization
C. space quantization
D. magnetic orbital quantization
E. that particles behave like waves
Check your answer: C. space quantization
Practice 8.1.4
The magnitude of the spin angular momentum for an electron is equal to
A.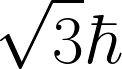
B.
C.
D.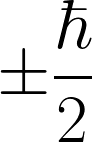
E.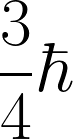
Check your answer: B